Everything about Heap data-structure

A heap is a specialized tree-based data structure which is essentially an almost complete tree that satisfies the heap property:

in a max heap, for any given node C, if P is a parent node of C, then the key (the value) of P is greater than or equal to the key of C.
in a min heap, the key of P is less than or equal to the key of C.

The node at the “top” of the heap (with no parents) is called the root node.

Heaps are usually implemented with an array, as follows:

Each element in the array represents a node of the heap, and
The parent / child relationship is defined implicitly by the elements’ indices in the array.

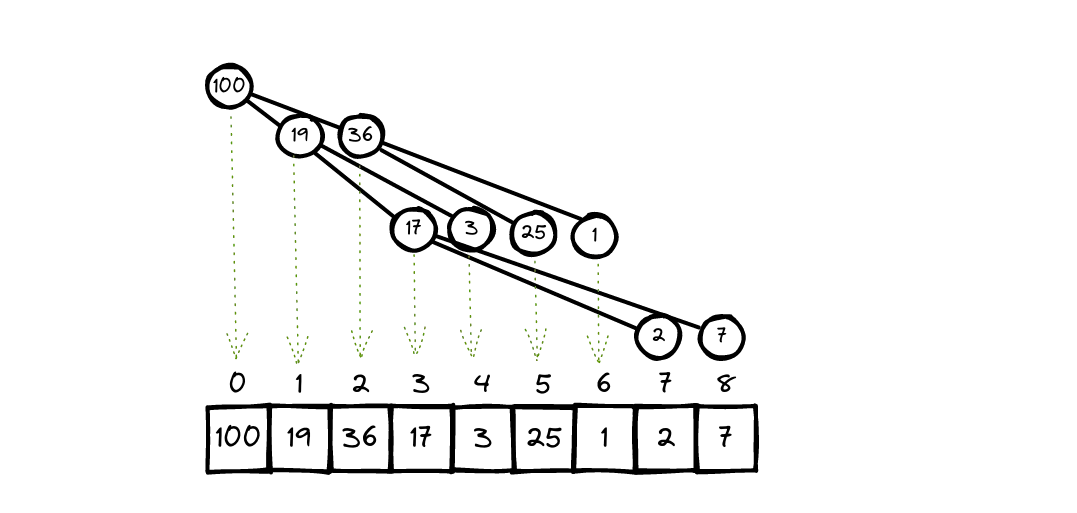
Given a node at index i,

its children are at indices 2i + 1 and 2i + 2, and
its parent is at index floor((i-1)/2)

Building heap

1
2
3
4
5
6
BUILD-HEAP(A)
    heapsize := size(A);
    for i := floor(heapsize/2) downto 1
        do HEAPIFY(A, i);
    end for
END

Time Complexity:

build_heap takes O(n) time complexity but heap_sort takes O(nlog(n)) time complexity.

We call heapify, which takes log(n), for n elements, but the time complexity of building heap comes out to be O(n).
The main idea is that in the build_heap algorithm the actual heapify cost is not O(log(n))for all elements.

Operations

The common operations involving heaps are:

Basic

find-max (or find-min):
find a maximum item of a max-heap, or a minimum item of a min-heap, respectively (a.k.a. peek)
insert:
adding a new key to the heap (a.k.a., push)
extract-max (or extract-min):
returns the node of maximum value from a max heap [or minimum value from a min heap] after removing it from the heap (a.k.a., pop)
delete-max (or delete-min):
removing the root node of a max heap (or min heap), respectively
replace:
pop root and push a new key. More efficient than pop followed by push, since only need to balance once, not twice, and appropriate for fixed-size heaps.

Creation

create-heap:
create an empty heap
heapify:
create a heap out of given array of elements
merge (union):
joining two heaps to form a valid new heap containing all the elements of both, preserving the original heaps.
meld:
joining two heaps to form a valid new heap containing all the elements of both, destroying the original heaps.

Inspection

size:
return the number of items in the heap.
is-empty:
return true if the heap is empty, false otherwise.

Internal

increase-key or decrease-key:
updating a key within a max- or min-heap, respectively
delete:
delete an arbitrary node (followed by moving last node and sifting to maintain heap)
sift-up:
move a node up in the tree, as long as needed; used to restore heap condition after insertion. Called “sift” because node moves up the tree until it reaches the correct level, as in a sieve.
sift-down:
move a node down in the tree, similar to sift-up; used to restore heap condition after deletion or replacement.

Variants

Operation	find-max	delete-max	insert	increase-key	meld
Binary	Θ(1)	Θ(log n)	O(log n)	O(log n)	Θ(n)
Binomial	Θ(1)	Θ(log n)	Θ(1)	Θ(log n)	O(log n)
Fibonacci	Θ(1)	O(log n)	Θ(1)	Θ(1)	Θ(1)

Applications

Heapsort
Priority queues can be efficiently implemented using Binary Heap.
- Heap Implemented priority queues are used in Graph algorithms like Prim’s Algorithm and Dijkstra’s algorithm.
Binomial Heap and Fibonacci Heap are variations of Binary Heap. These variations perform union also in O(logn) time which is a O(n) operation in Binary Heap.
Order Statistics: The Heap data structure can be used to efficiently find the kth smallest (or largest) element in an array. https://en.wikipedia.org/wiki/K-way_merge_algorithm

MinHeap Implementation in Python

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
# Python3 implementation of Min Heap

import sys


class MinHeap:
    def __init__(self, max_size):
        self.max_size = max_size
        self.size = 0
        self.heap = [0] * (self.max_size + 1)
        self.heap[0] = -1 * sys.maxsize
        self.FRONT = 1

    # Function to return the position of
    # parent for the node currently
    # at pos
    def parent(self, pos):
        return pos // 2

    # Function to return the position of
    # the left child for the node currently
    # at pos
    def left_child(self, pos):
        return 2 * pos

    # Function to return the position of
    # the right child for the node currently
    # at pos
    def right_child(self, pos):
        return (2 * pos) + 1

    # Function that returns true if the passed
    # node is a leaf node
    def is_leaf(self, pos):
        if pos >= (self.size // 2) and pos <= self.size:
            return True
        return False

    # Function to swap two nodes of the heap
    def swap(self, fpos, spos):
        self.heap[fpos], self.heap[spos] = self.heap[spos], self.heap[fpos]

    # Function to heapify the node at pos
    def min_heapify(self, pos):

        # If the node is a non-leaf node and greater
        # than any of its child
        if not self.is_leaf(pos):
            if (
                self.heap[pos] > self.heap[self.left_child(pos)]
                or self.heap[pos] > self.heap[self.right_child(pos)]
            ):

                # Swap with the left child and heapify
                # the left child
                if self.heap[self.left_child(pos)] < self.heap[self.right_child(pos)]:
                    self.swap(pos, self.left_child(pos))
                    self.min_heapify(self.left_child(pos))

                # Swap with the right child and heapify
                # the right child
                else:
                    self.swap(pos, self.right_child(pos))
                    self.min_heapify(self.right_child(pos))

    # Function to insert a node into the heap
    def insert(self, element):
        if self.size >= self.max_size:
            return
        self.size += 1
        self.heap[self.size] = element

        current = self.size

        while self.heap[current] < self.heap[self.parent(current)]:
            self.swap(current, self.parent(current))
            current = self.parent(current)

    # Function to print the contents of the heap
    def print(self):
        for i in range(1, (self.size // 2) + 1):
            print(
                " PARENT : "
                + str(self.heap[i])
                + " LEFT CHILD : "
                + str(self.heap[2 * i])
                + " RIGHT CHILD : "
                + str(self.heap[2 * i + 1])
            )

    # Function to build the min heap using
    # the min_heapify function
    def min_heap(self):

        for pos in range(self.size // 2, 0, -1):
            self.min_heapify(pos)

    # Function to remove and return the minimum
    # element from the heap
    def remove(self):

        popped = self.heap[self.FRONT]
        self.heap[self.FRONT] = self.heap[self.size]
        self.size -= 1
        self.min_heapify(self.FRONT)
        return popped


# Driver Code
if __name__ == "__main__":

    print("The minHeap is ")
    minHeap = MinHeap(15)
    minHeap.insert(5)
    minHeap.insert(3)
    minHeap.insert(17)
    minHeap.insert(10)
    minHeap.insert(84)
    minHeap.insert(19)
    minHeap.insert(6)
    minHeap.insert(22)
    minHeap.insert(9)
    minHeap.min_heap()

    minHeap.print()
    print("The min value is " + str(minHeap.remove()))

Using Python’s heapq library

heapq implements min_heap, see code below:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
import heapq

# initializing list
li = [5, 7, 9, 1, 3]

# using heapify to convert list into heap
heapq.heapify(li)

# printing created heap
print(list(li))

# using heappush() to push elements into heap
heapq.heappush(li, 4)

# using heappop() to pop smallest element
print(heapq.heappop(li))

Kth largest or smallest

Do not use this when doing heap problems this creates a min heap everytime

1
2
3
4
5
6
# using nlargest to print 3 largest numbers
# this returns a list which is sorted
print(heapq.nlargest(3, li1, key= lambda x:x))

# using nsmallest to print 3 smallest numbers
print(heapq.nsmallest(3, li1, key= lambda x:x))

Implement `max_heap` with `heapq`

This library supports min_heap implementation, to make max_heap multiply each element with -1

Push custom object with `heapq`

If the object implements comparison operators, you can push your custom objects into the heap.
In case you are not able to update/implement class definition, you can use tuple to push custom objects, wherein the first member of the tuple is the comparison key.
eg: heapq.heappush(heap, (l.val, l)), here l is a class object (lets say linked-list)
The problem with putting (l.val, l) on the heap is that when two tuples’s first member have the same value, then a comparison will happen between the second member values, i.e. between l class objects.
Either make sure your first member will never have a conflict (this shall throw runtime error) or you can introduce a third member (unique value) in those tuples, between the two members you already have.
eg: heapq.heappush(heap, (l.val, i, l))
But remember if the second member will have conflict this too shall throw runtime error.

Sources:

https://docs.python.org/3/library/heapq.html